| Definition. A function F is an antiderivative or an indefinite integral of the function f if the derivative F' = f.
We use the notation

to indicate that Fis an indefinite integral of f. Using this notation, we have
 if and only if if and only if 
| |
Definite vs. Indefinite: The difference between the two types of integrals is that with Definite integrals, you can find the area underneath a graph that may also be bounded by curves and lines. With those types of integrals, you are also given upper and lower bounds. With Indefinite integrals, you are not given any bounds. Those types of integrals are worked out for the sake of working them out and not solving them after antidifferentiation.
Definite Integrals
| Definition. Let f be a function which is continuous on the closed interval [a, b]. The definite integral of f from a to b is defined to be the limit

where

| |
Theorem. If f (x) and g(x) are defined and continuous on [a, b], except maybe at a finite number of points, then we have the following linearity principle for the integral:
- (i)
  f (x) + g(x) f (x) + g(x) dx = dx =  f (x) dx + f (x) dx +  g(x) dx; g(x) dx;
- (ii)
  f (x) dx = f (x) dx =   f (x) dx, for any arbitrary number f (x) dx, for any arbitrary number  . .
The next results are very useful in many problems.
Theorem. If f (x) is defined and continuous on [a, b], except maybe at a finite number of points, then we have
- (i)
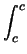 f (x) dx = 0; f (x) dx = 0;
- (ii)
 f (x) dx = f (x) dx = 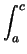 f (x) dx + f (x) dx + 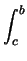 f (x) dx; f (x) dx;
- (iii)
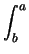 f (x) dx = - f (x) dx = -  f (x) dx; f (x) dx; -
-
^^A great animation for Integral Funtions^^
|
Definite Integrals
As an example, note that since

it follows that

| |
|
These examples focus upon a specific type of antiderivative, which is the Indefinite kind. In this case, no bounds are set for the function being antidifferentiated. |
|


