Integral Calculus 2
Integration Techniques
Power Rule for Integration:
Given a rational number n different from -1, then

where du = u' dx.
U-Substitution:
Trigonometric Integration:
| [integral] arcsin x dx = x arcsin x + [sqrt](1-x^{2}) + C |
| [integral] arccsc x dx = x arccos x - [sqrt](1-x^{2}) + C |
| [integral] arctan x dx = x arctan x - (1/2) ln(1+x^{2}) + C |
Rules for Integration involving log functions
Natural log: 
Other Rules for Natural Logs include:
- ln (a*b) = ln (a) + ln (b)
- ln (a) - ln (b) = ln (a/b)
- ln (a^b) = b*ln (a)
Net vs. Total Area:
- Net Area pertains to the area accounted for above the graph minus the area below the graph. It is true that the area above the graph is positive while the area below is negative and so if the graph of a function has equal area above and below the x-axis, then its Net Area is zero.
- Total Area differs from Net Area because it doesn't look at where the area of the graph lies, whether it be above or below the x-axis. If the graph has area above or below the x-axis, then its Total Area is just all of that area accounted for added up.
The Theorems of Calculus
The First Fundamental Theorem of Calculus
Theorem. Let f be a function which is continuous on the interval [a, b].
- Let F be an indefinite integral or antiderivative of f. Then

- The function

is an indefinite integral or antiderivative of f. That is,
A'(x) = f(x)
| |

The animation shows the area bounded by the thin yellow line which is the graph of y = sin(t), the t-axis, and the line t=x for various increasing values of x. The thick yellow line is the graph of y = F(x), the area function.
Another explanation and example can be found here
Example:
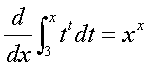
Example:
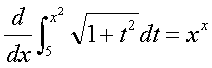
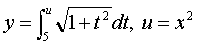
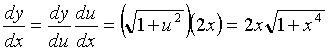
Riemann Sums:

LRAM, MRAM, RRAM, and Trapezoids
Riemann Sums
Suppose that a function f is continuous and non-negative on an interval [a,b]. Let's compute the area of the region R bounded above by the curve y = f(x), below by the x-axis, and on the sides by the lines x = a and x = b.

We will obtain this area as the limit of a sum of areas of rectangles as follows:
First, we will divide the interval [a,b] into n subintervals
| [x0, x1], [x1, x2], ¼, [xn-1, xn] |
where a = x0 < x1 < ¼ < xn = b. (This is called a partition of the interval.) The intervals need not all be the same length, so call the lengths of the intervals Dx1, Dx2, ..., Dxn, respectively. This partition divides the region R into n strips.

Next, let's approximate each strip by a rectangle with height equal to the height of the curve y = f(x) at some arbitrary point in the subinterval. That is, for the first subinterval [x0, x1], select some x1* contained in that subinterval and use f(x1*) as the height of the first rectangle. The area of that rectangle is then f(x1*) Dx1.

Similarly, for each subinterval [xi-1, xi], we will choose some xi* and calculate the area of the corresponding rectangle to be f(xi*) Dxi. The approximate area of the region R is then the sum åin= 1 f(xi*) Dxi of these rectangles.

Depending on what points we select for the xi*, our estimate may be too large or too small. For example, if we choose each xi* to be the point in its subinterval giving the maximum height, we will overestimate the area of R. (This is called an upper sum.)

If, on the other hand, we choose each xi* to be the point in its subinterval giving the mimimum height, we will underestimate the area of R. (This is called a lower sum.)

When the points xi* are chosen randomly, the sum åin= 1 f(xi*) Dxi is called a Riemann Sum

and will give an approximation for the area of R that is in between the lower and upper sums. The upper and lower sums may be considered specific Riemann sums.
As we decrease the widths of the rectangles, we expect to be able to approximate the area of R better. In fact, as max Dxi ® 0, we get the exact area of R, which we denote by the definite integral
ó
õ |
b
a
|
f(x) dx . |
That is,
ó
õ |
b
a
|
f(x) dx = limmax Dxi® 0 |
æ
ç
è |
n
Ã¥
i = 1
|
f(xi*)Dxi |
ö
÷
ø |
Notes
-
This definition of the definite integral still holds if f(x) assumes both positive and negative values on [a, b]. If even holds if f(x) has finitely many discontinuities but is bounded.
-
For a more rigorous treatment of Riemann sums, consult your calculus text.
The following Exploration allows you to approximate the area under various curves under the interval [0, 5]. You can create a partition of the interval and view an upper sum, a lower sum, or another Riemann sum using that partition. The Exploration will give you the exact area and calculate the area of your approximation. To create a partition, choose which type of sum you would like to see and click the mouse between the partition labels x0 and x1
Applet:
Animation:
Double Click to View the Above Animation!
Trapezoid Rule
Since we have not properly covered the Trapezoid Rule as well as the LRAM, MRAM, and RRAM techniques, the following example does a great job on showing the significance of trapezoids in area approximation.
Problem:
Graphically illustrate the approximation of the integral

using the Trapezoidal Rule.
Visualization:

[Press this to see animation again!]
In the animation above, first you can see how by increasing the number of equal-sized intervals the sum of the areas of trapezoids can better approximate the integral.
The following table indicates the sums of the various areas of the trapezoids n indicates the number of trapezoids.
| n |
Sum of areas of
trapezoids |
| 4 |
0.43358 |
| 8 |
0.70404 |
| 16 |
0.75723 |
| 32 |
0.76954 |
| 64 |
0.77256 |
| 128 |
0.77331 |
| 256 |
0.77350 |
| 512 |
0.77355 |
| 1024 |
0.77356 |
| 2048 |
0.77356 | |
0.77356 appears to be a reasonable estimate of our integral.
|


