Rolle's Theorem. Let f be a function which is differentiable on the closed interval [a, b]. If f(a) = f(b) then there exists a point c in (a, b) such that f '(c) = 0.

Implicit Differentiation

In many examples, especially the ones derived from differential equations, the variables involved are not linked to each other in an explicit way. Most of the time, they are linked through an implicit formula, like F(x,y) =0. Once x is fixed, we may find y through numerical computations. (By some fancy theorems, we may formally show that y may indeed be seen as a function of x over a certain interval). The question becomes what is the derivative 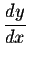, at least at a certain a point? The method of implicit differentiation answers this concern.

Example:

Example. Find the equation of the tangent line to the ellipse

at the point (2,3). One way is to find y as a function of x from the above equation, then differentiate to find the slope of the tangent line. We will leave it to the reader to do the details of the calculations. Here, we will use a different method. In the above equation, consider y as a function of x:

and use the techniques of differentiation, to get

From this, we obtain

which implies that 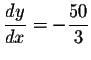at the point (2,3). So the equation of the tangent line is given by

or equivalently

You may wonder why bother if this is just a different way of finding the derivative? Consider the following example! It can be very hard or in fact impossible to solve explicitly for y as a function of x.