|
Variations In Limits
Limits of Trigonometric Functions: 
Limit of Sine Demonstration
**Tangent & Cosine rules and General Rules for Limits to come..**
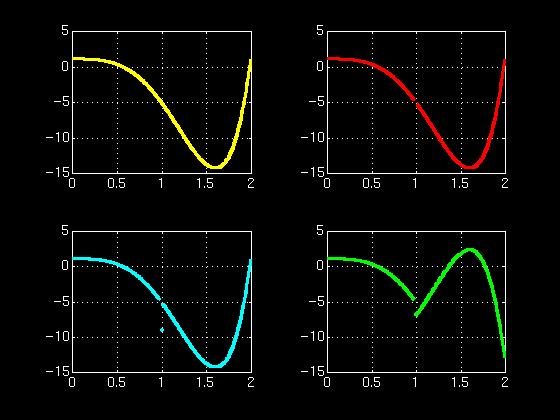
The first three functions all have limit -5 as x approaches 1, emphasizing the irrelevance of the value of the function at the limit point itself. The last function has different left and right hand limits at 1, and so the limit does not exist.
Right-hand derivative |
 |
Left-hand derivative |
 |
This function f(x) is not differentiable at x = a .
Because right-hand derivative is not left-hand derivative. |

Contact Me
Flash Movie On Limits
Movie Time!! |


